"CAL-Q-ABLE" is an educational game for all ages, using numbers, and can be played by 2, 3 or 4 players.
"CAL-Q-ABLE" will assist in better understanding and knowledge in the use of numbers and will contribute towards an improvement in mental arithmetic.
The game consists of forming numerical equations, either across or down the "CAL-Q-ABLE" playing board using the numbered tiles which have a score value alloted to each tile.
Each player tries to get a high score with his equation In combinations and situations to give him the best advantage of number values and premium squares.
Every tile in "CAL-Q-ABLE" has a value number printed on the tile, this being the small number which is used when calculating the score value of your equation.
TO BEGIN
START OF PLAY
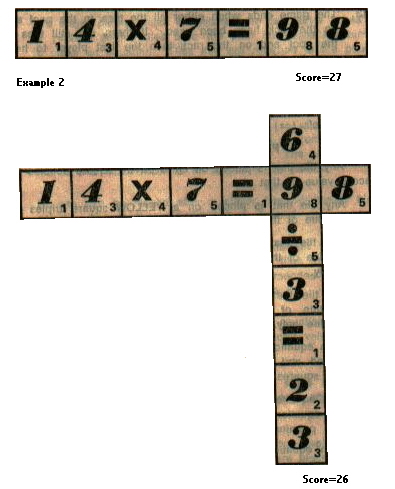
1. The first player makes an equation with his tiles but one of the tiles in the equation must go on the square which has the Brain Grain-Games Logo on it and the equation can be pieced either across or down the playing board. After the first move the next player must include In his equation one of the tiles of the previously formed equation (see example 2) and succeeding players can then move with their equation. Every equation placed on the playing board must include any one of the tiles in an equation already on the playing board.
2. A player completes his turn by counting the total value of the small numbers on each tile of the equation he has played on the playing board Including the value of the premium squares covered by the equation.
3. The score is put on the scoring pad and he then replaces from the pool the number of tiles used in his equation so that he still has nine tiles on his rack in readiness for his next turn. The player on his left then takes his turn and the play continues in that direction.
4. If a player cannot make an equation he can either "pass" or replace all his tiles from the pool but loses his turn to make an equation. Tiles that are returned to the pool must be well shuffled in with the other tiles in the pool.
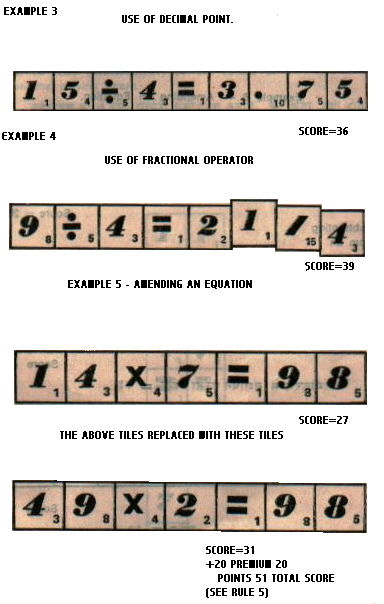
5. A player may remove from the board all the tiles in front of an equals (=) sign and replace with other tiles from his rack but the answer to the equation so altered must be the same (see Example 5). All tiles so removed are returned to the pool and shuffled well in. The player who makes this move receives an additional 20 points.
6. No tile can be moved after a player has completed his equation except that as provided by Rule 5.
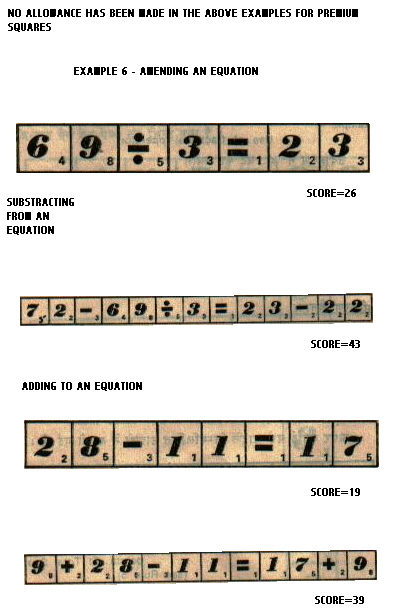
7. A player can, In his turn, add to or subtract from, any equation on the playing board with his tiles and scores the total value of all the tiles on the amended equation, including premium squares (see example 6).
8. If a player uses all his nine tiles in an equation then he scores an additional 50 points to the total value of his equation.
9. No equation can have two equals (=) signs as, to be mathematically correct, there is only one equals (=) sign in an equation.
10.When making an equation in which the fractions (I) sign is used all the tiles in the fraction are placed slightly below the line (see Example 4).
11.The lowest common denominator is not compulsory when making an equation in which the answer has tractions, I.e. 12 divided by 5 can be, in the answer, expressed as 2 and 2/5, or 2 and 4/10, or 2 and 8/20. The formation of an equation in which the fractions sign is used depends upon the tiles in the player’s raclc which are availabie for such an equation.
12.No equation can be placed on the playing board which does not cross an existing equation (see Example 7). For clarification of this rule refer to Rule 1.
13.The game ends when either all the tiles in the pool and on the rack have been used. If there are still tiles in the pool and on the rack then the last player to have moved adds to his score the value of the tiles on the other player’s racks. The player with the highest score at the end of the game is declared the winner.
14.The game can be shortened by removing some of the equals (=) signs from the pool.
PREMIUM NUMBER SQUARES
Any tile that is placed on an ORANGE square doubles the score value of that tile.
Any tile that is placed on a YELLOW square triples the score value of that tile.
Any tile that is placed on a BLUE square doubles the score value of that equation including premium squares, score value only.
Any tile that is placed on a GREEN square triples the score value of that equation, including premium squares, score value only.
If an equation covers two BLUE squares then the equation is doubled and then re-doubled, score value only, Including premium squares.
If an equation covers a BLUE square and a GREEN square then the equation is doubled and then tripled, score value only, including premium squares.
If an equation covers two GREEN squares then the score value of that equation, including premium squares is tripled, then that score is tripled again.
For a more advanced game players can increase the number of white tiles to nine and grey tiles to three making twelve tiles to start the game with.
CAL-Q-ABLE